Institut für Rechnerentwurf und Fehlertoleranz
- Universität Karlsruhe
Forschungsschwerpunkt Informationslogistik
Ereignisorientierte Simulation
Überblick Ereignisorientierte
Simulation eines Warteschlangenmodells Software-Voraussetzungen
Zurück zur Modellierungsseite
Überblick
Bei vielen Prozessen, vor allem in betrieblich-organisatorischen Systemen,
z.B. bei Abläufen in Produktions-, Transport-, oder Lagerhaltungssystemen,
ändert sich der Systemzustand nicht kontinuierlich, sondern diskret.
Ein gutes Beispiel für ein solches System ist die Warteschlange vor
einer Maschinengruppe einer Fertigungsanlage: Der Zustand der Warteschlange
(die Zahl der "wartenden" Werkstücke) ändert sich nur bei Ankunft
oder Abgang eines Werkstücks. Diese Ankünfte und Abgänge
können als diskrete Ereignisse betrachtet werden, d.h. als
Ereignisse, die zu diskret über die Zeitachse verteilten Zeitpunkten
auftreten. Bei Systemen, wo primär das Interesse auf den Ereignissen
liegt, hat man es im wesentlichen mit logischen Gleichungen zu tun, welche
die Bedingungen für das Eintreten der Ereignisse enthalten. Die Simulation
besteht hier in der Beobachtung von Zustandsänderungen des Modells
als Folge zeitdiskret auftretender Ereignisse. Solche Simulationen werden
auch diskrete Simulationen genannt. Da dieser Modellansatz eine
Diskretisierung der Zeit und damit eine bestimmte Betrachtungsweise der
Realsysteme voraussetzt, spricht man auch von der Simulation zeitdiskreter
Systeme.
Zeitdiskrete Simulationsmodelle treten in vielfältigen
Formen auf und werden für die unterschiedlichsten Problemstellungen
eingesetzt. Innerhalb der zeitdiskreten Simulation haben sich verschiedene
konzeptuelle Sichtweisen herausgebildet, wobei der ereignisorientierte
Ansatz heute den wohl wichtigsten und am weitesten verbreiteten Modellierungsstil
darstellt.
Bei der diskreten Ereignis-Simulation (discrete
event simulation) wird eine modellinterne Simulationsuhr von der
Ablaufkontrolle jeweils bis zum nächstfolgenden Ereigniszeitpunkt
vorgerückt. Dies impliziert, daß die Zeit zwischen zwei benachbarten
Ereignissen im allgemeinen variabel ist. Der Simulationszeitpunkt eines
Ereignisses kann beliebig gewählt werden, wodurch eine wirklichkeitsgetreue
Abbildung der Zustandsänderungen möglich ist. Dies wäre
nicht der Fall, wenn man die Simulationsuhr in konstanten Zeitintervallen
weiterschalten würde. Dann müßten alle Ereigniszeitpunkte
auf das Ende eines solchen Intervalls verschoben werden, was bei ungünstiger
Wahl der Schrittlänge erhebliche Verfälschungen des Modellverhaltens
bewirken kann.
Bei der diskreten Ereignis-Simulation ist es durchaus
möglich, daß Ereignisse simultan auftreten, also in einem Ereigniszeitpunkt
zusammenfallen. Ein sequentiell arbeitender Rechner ist jedoch nur in der
Lage, die Ereignisse (Zustandsänderungen) nacheinander abzuarbeiten.
Das erzwingt eine Sequentialisierung paralleler Ereignisse. Hierfür
wird von den ereignisorientierten Simulationssprachen in der Regel ein
Prioritätsmechanismus bereitgestellt.
Grundsätzlich beruht der ereignisorientierte
Ansatz auf einer detaillierten Beschreibung von Ereignissen in Form von
Ereignisroutinen.
In einem ereignisorientierten Modell werden lediglich die Zustandsänderungen
nachvollzogen, die zu den Ereigniszeitpunkten stattfinden, nicht jedoch
die Tätigkeiten, die in den dazwischenliegenden Intervallen ablaufen.
Zeitlich ausgedehnte Vorgänge werden somit auf eine Folge von Ereignissen
reduziert, von denen jedes einzelne einem Punkt auf der Zeitachse (dem
Ereigniszeitpunkt) zugeordnet ist. Unabhängig davon, wieviel Rechenzeit
zur Ausführung einer Ereignisroutine auf einem Computer real verbraucht
wird, geschieht sie konzeptuell zeitverzugslos. Die interene Simulationsuhr
wird vor der Ausführung der Ereignisroutine zum Ereigniszeitpunkt
vorgestellt, steht während der Ausführung still und springt nach
vollzogener Zustandsänderung auf den Zeitpunkt des nächsten Ereignisses
vor.
Mit der vorliegenden Animation sollen die grundlegenden
Abläufe und Vorgänge bei der ereignisorientierten Simulation
verdeutlicht werden.
Ereignisorientierte Simulation eines
erweiterten Warteschlangenmodells
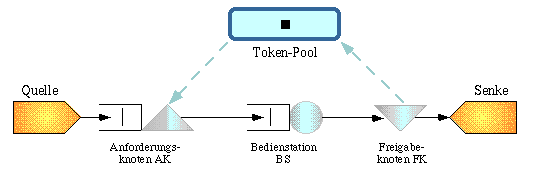
In Abb. 1 ist ein sehr einfaches erweitertes Warteschlangenmodell
dargestellt, mit dem die Pufferung und Verarbeitung von Datenpaketen
in Kommunikationssystemen nachgebildet wird. Datenpakete werden von der
Quelle mit einer bestimmten Ankunftsrate erzeugt. Ein erzeugtes Datenpaket
wird zum Anforderungsknoten AK weitergeleitet, an dem es Pufferspeicher
beansprucht. Der Pufferspeicher wird durch die im Token-Pool vorhandene
Marke modelliert. Nach der Tokenübernahme wird das Datenpaket zur
Bedienstation BS weitergereicht, die mit einer bestimmten Bedienrate Datenpakete
abarbeitet. Ist die Verarbeitung des Datenpakets abgeschlossen, wird die
beanspruchte Marke im Freigabeknoten FK wieder in den Token-Pool zurückgelegt.
Anschließend verläßt das Datenpaket das Warteschlangennetz
in der Senke.
|
Abb. 1: Erweitertes Warteschlangenmodell zur Modellierung der Pufferung
und Verarbeitung von Datenpaketen
Animation
der ereignisorientierten Simulation des erweiterten Warteschlangenmodells
Software-Voraussetzungen zur Betrachtung
der Animation
Zur Betrachtung der Animation wird die Multimediaerweiterung QuickTime
3 der Firma Apple Computer benötigt. Diese kann im WWW
unter der Adresse "http://www.apple.com/quicktime/download/index.html"
heruntergeladen werden. Falls nicht vorhanden, werden Sie beim Aufruf der
Animation aufgefordert, dieses Plugin zu installieren.

