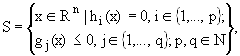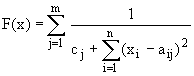JAVA-BASED ANIMATION OF PROBABILISTIC SEARCH ALGORITHMS

Michael Syrjakow

Institute for Computer Design and
Fault Tolerance (Prof. D. Schmid)
University of Karlsruhe
76128 Karlsruhe
P.O. Box 6980, Germany
syrjakow@ira.uka.de

Helena Szczerbicka

Department of Computer Science
(Fb3 Informatik)
University of Bremen
28334 Bremen
P.O. Box 330440, Germany
helena@informatik.uni-bremen.de

Paper in postscript format

KEYWORDS

Probabilistic Search Algorithms, Genetic Algorithms, Software Animation, Java, Parameter Optimization of Simulation Models.

ABSTRACT

This paper describes a flexible Java-based animation environment for probabilistic optimization methods. Within the simulation area probabilistic search techniques like Genetic Algorithms, Evolution Strategies, and Simulated Annealing have gained great importance, particularly for parameter optimization of simulation models. A fundamental drawback of these methods however is their complicated handling. Especially inexperienced users have a lot of difficulties in parameterizing the stochastic operators in order to adapt the search algorithm optimally to a specific problem. One of the main objectives of the animation environment presented in this paper is to facilitate the understanding of the sophisticated search processes within probabilistic search algorithms. The capabilities of our developed animation environment are demonstrated by means of a comprehensive animation example. In this example the stochastic search process of a Genetic Algorithm is visualized.

INTRODUCTION
REAL PARAMETER OPTIMIZATION
GENETIC ALGORITHMS
JAVA-BASED ANIMATION OF GAs
AN ANIMATION EXAMPLE
CONCLUSIONS
ACKNOWLEDGEMENTS
REFERENCES
BIOGRAPHY

INTRODUCTION

During the last three decades probabilistic search methods have gained great importance in global optimization. Some well-known representatives are Genetic Algorithms GA (Goldberg 1989), Evolution Strategies ES (Schwefel 1981) and Simulated Annealing SA (Aarts and Korst 1990). All these methods extensively apply probabilistic search operators which are based on principles of nature. Another very important property of these methods is that they use nothing but goal function values for orientation. Search algorithms with this property are called direct optimization methods. Compared to traditional mathematical optimization techniques direct search strategies have the advantage that derivatives or other auxiliary knowledge about the optimized goal function is not required. This makes direct search general applicable and predestinate to black box optimization. In our research work direct optimization algorithms have been applied very successfully to parameter optimization of simulation models (Syrjakow and Szczerbicka 1995).

This paper describes a Java-based approach for animation of the complex search process performed by probabilistic optimization methods. The main objectives of our approach are

to gain a better insight into the sophisticated working mechanisms of probabilistic optimization methods;
to offer inexperienced users the possibility to properly deal with these methods (to get a feeling for a good parameterization of their probabilistic search operators);
to acquire fundamental knowledge which enables to further enhance the performance of probabilistic search methods.

The paper is organized as follows: First of all we introduce into real parameter optimization. After that Genetic Algorithms being a well-known and wide-spread probabilistic search technique are described. Subsequently the software-architecture of a Java-based animation environment for probabilistic search methods is presented. The capabilities of this environment are demonstrated by means of a detailed animation example. Finally we summarize and draw some conclusions.

REAL PARAMETER OPTIMIZATION

In this paper real parameter optimization problems are considered which can be formalized as tupels (S,F). The solution space S denotes the set of all possible problem solutions. Every solution from S is valued by a goal function F: S® R. For unconstrained parameter optimization problems S = Rⁿ, otherwise:

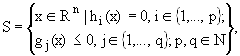
h_i: Rⁿ®R equality constraints
g_j: Rⁿ® R inequality constraints

The overall goal of global parameter optimization is to find a vector x*ÎS which satisfies:

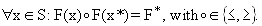
A solution x* is called global optimum point. The function value F(x*)=F^* is referred to as global optimum of F. Beside global optimum points there may exist local optimum points x^Ù, having the property that all neighbouring solutions have the equal or a worse goal function value. An optimization problem is either a minimization (o =³ ) or a maximization (o =£ ) problem. Minimization problems can be easily transformed into maximization problems and vice versa, because

min{F(x)} = -max{- F(x)}.

The mathematical optimization problem (S,F) which is used for maximization in our animation example is defined in Table 1. The goal function F is an often used benchmark function for direct optimization algorithms. Functions of this type are called Shekel-functions (Shekel 1971).

Search space
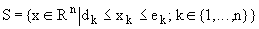Goal function

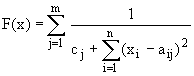Table 1: Mathematical representation of the optimization
problem used in the animation example of this paper

d_k<e_k; kÎ{1,...,n}, nÎN represent the interval borders of the n-dimensional search space S. a_ij; iÎ{1,....,n}, jÎ{1,....,m}, mÎN determine the coordinates of the m maximum points of (S,F). With the constants c_j; jÎ{1,...,m} the goal function values of the maximum points of (S,F) are adjusted.

Because our visual imagination is limited to three dimensions our animation environment is restricted to visualization of search processes within 2-dimensional search spaces. Fig. 1 shows a 3D-representation of an instance of a 2-dimensional Shekel-function. The function surface looks like a mountain range comprising one global maximum point x*=(4,4) and nine local ones.

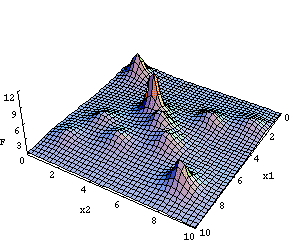
Fig. 1: Graphical 3D-representation of an instance of a
2-dimensional Shekel-function with 10 maximum points

GENETIC ALGORITHMS

In this paper we focus on Genetic Algorithms (Goldberg 1989; Michalewicz 1992) which represent a very common and wide-spread probabilistic search method. In the following some fundamentals of Genetic Algorithms are described. This class of algorithms which is based on the principles of natural evolution maintains a population

P(t) = {s₁^t,s₂^t,...,s_p^t}

of individuals s_j^t, jÎ{1,...,p}; t,pÎN. Each individual s_j^t is implemented as a fixed-length binary string (a so-called chromosome) and represents a potential solution of the optimization problem (S,F) which has to be solved. In case of real parameter optimization the binary string is locally divided into segments, each containing the binary code of the corresponding parameter value. The upper t represents the iteration step (actual generation). The goal of the Genetic Algorithm is to evolve through alternation in generations towards better and better regions of the search space. The alternation is done by application of probabilistic genetic operators (selection, crossover, and mutation).

With selection poor solutions (individuals with low fitness) are sorted out of a population. For that reason, this operator can be viewed as an artificial version of natural selection (a realization of the Darwinian principle "survival of the fittest" among string creatures). The fitness of an individual is calculated by evaluation of the goal function F of the optimization problem. After selection the probabilistic recombination operators crossover and mutation are applied to generate new solutions for the next generation of individuals which is evaluated again in the subsequent iteration step. The basic structure of a Genetic Algorithm is shown in Fig. 2.

procedure Genetic Algorithm;
begin

t:=0;
initialize P(t);
evaluate P(t);
while (not termination-condition) do
begin
t:=t+1;
select P(t) from P(t-1);
recombine P(t);
evaluate P(t);
end;

end;

Fig. 2: Basic structure of a Genetic Algorithm

For a more detailed description of Genetic Algorithms we refer to (Goldberg 1989; Michalewicz 1992).

JAVA-BASED ANIMATION OF GAs

The past experience gathered in the field of software visualization (Stasko et al. 1998) has shown that the realization of illustrative computer animations usually is very expensive. For that reason the implementation of powerful animations only makes sense if they are used within a broad application field. We intend to use our animations

to support our own research activities;
for teaching our students;
for an illustrative demonstration of our research work on the World Wide Web.

In order to achieve the purposes above we have decided to use Java as the programming language for implementation of our animations. The main reasons for this decision are the following:

Java is familiar and simple

Java is based on C++ while removing its complex, dangerous, and superfluous elements.

Java is object-oriented

Java provides all the advantages of object-oriented programming like class hierarchy, inheritance, encapsulation, polymorphism, etc.

Java provides a powerful set of class libraries

The Java API (Application Programming Interface) includes standard packages for developing window programs, applets, client server networking software, etc.

Java is platform independent

Today there exist Java-interpreters for many operating systems including Solaris, Windows and MacOS.

Java is multithreaded

Java provides built-in language support for multithreading.

Java is the programming language of the World Wide Web

Today Java can be viewed as the first Web programming language and the most powerful tool to develop platform-independent software.

Architecture

In the following the software-architecture of our Java-based animation environment for probabilistic search methods is described. The basic components of this system are shown in Fig. 3.

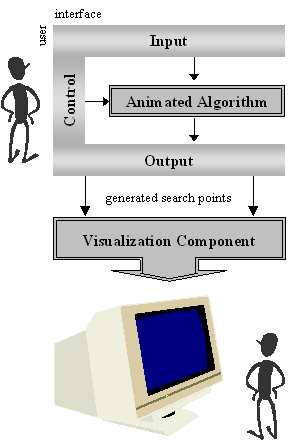
Fig. 3: SW-architecture of the animation environment
for probabilistic search algorithms

The probabilistic search algorithm which has to be animated is surrounded by a graphical user interface. This interface comprises an input-, control-, and an output part. The input part allows the user to parameterize the search algorithm. Parameterization is very important because our animations are intended to be objects for exhaustive studies. In addition to that the user should be able to interactively control the running optimization process (start, stop, switch into a step mode, etc.). This can be done using the control part. The task of the output part is to transfer the computed data of the animated optimization algorithm to the visualization component where it is prepared for visualization on the screen.

The Visualization Component

Outgoing from the output data (search points) computed by the animated optimization algorithm the task of the visualization component is to make the running optimization process visible on the screen. An important design goal was to realize a flexible visualization component which should be applicable to all kinds of iteratively working direct optimization methods (point-to-point but also population-based strategies). Population-based methods like GA or ES generate a set (population) of search points in each iteration step whereas point-to-point strategies like SA or Hill Climbing compute exactly one point.

In order to keep the complexity of our visualization component low we restricted our considerations to 2-dimensional real parameter optimization problems with rectangular search spaces. In that special case the surface of the goal function can be easily represented by a density plot.

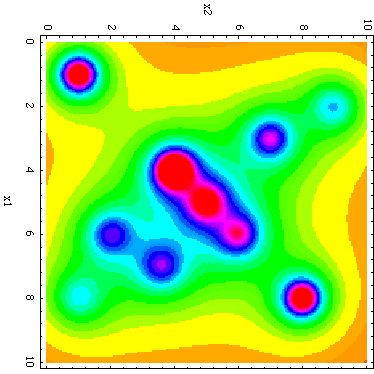
Fig. 4: Density plot of the Shekel-function

Fig. 4 shows a density plot of the Shekel-function presented in Fig. 1. For visualization of the running optimization process the generated search points are plotted directly upon the density plot. When the visualization component is applied to point-to-point methods the generated search points are plotted one after another without deletion of the former ones. This way it is possible to observe the development of the whole optimization trajectory (all generated search points). In case of population-based search however where the quickly growing optimization trajectory soon becomes very difficult to survey it makes more sense to plot the generated populations separately.

In the animation example presented in the following Section our animation environment is applied to visualize the probabilistic search process of a population-based Genetic Algorithm.

AN ANIMATION EXAMPLE

In this Section an animation example is described in detail in order to get an impression of the capabilities of our animation environment. In this example the probabilistic search process of a Genetic Algorithm is visualized. The task of the GA is to maximize the 2-dimensional Shekel-function shown in Fig. 1. After starting the animation which is implemented as a Java-applet the graphical user interface presented in Fig. 6 appears on the screen. The coloured square at the top shows the density plot of the Shekel-function being the playing ground for the GA. Underneath some information about the actual state of the optimization process is presented. The four buttons at the bottom allow

to start the animation

The GA search can be started by either pressing the "Start All" or the "Step by Step" button. The "Start All" button causes a complete animation run which is stopped not before the specified number of generations is reached (see Fig. 5). After each computed generation the actual distribution of its individuals is plotted upon the density plot. A few seconds later the animation automatically proceeds to the next generation. The "Step by Step" button allows to manually perform the animation stepwise. This enables the user to comprehensively analyze each animation step for an arbitrary amount of time.

to set the control parameters of the GA

The "Change Parameter" button gives the user the opportunity to manipulate the GA control parameters shown in Fig. 5.

to get a 3D-representation of the optimized goal function

The pressing of the "Show Function 3D" button activates a window with a graphical 3D-representation of the optimized goal function (here the Shekel-function shown in Fig. 1). In the following three different states of a typical animation run are presented. For parameterization of the GA we use the settings shown in Fig. 5 which are based on recommendations from literature (Schaffer et al. 1989).

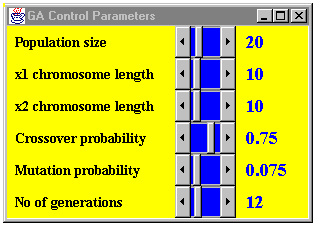
Fig. 5: Control parameter settings of the GA

Fig. 6 shows the optimization process just after computation of the initial population P(0). It is easy to see that a random number generator was used to distribute the 20 individuals of P(0) randomly all over the search space.

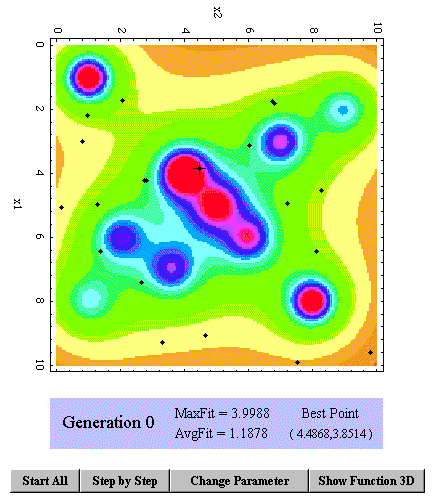
Fig. 6: Distribution of the individuals of the randomly generated population P(0)

Fig. 7 shows the distribution of the individuals of population P(6). Here we can easily recognize a tendency of convergence towards the region of the global optimum point which is located at (4,4).

Fig. 7: Distribution of the individuals of population P(6)

Fig. 8 shows the situation after 12 computed generations. Here almost half of the population is gathered around the global optimum point.

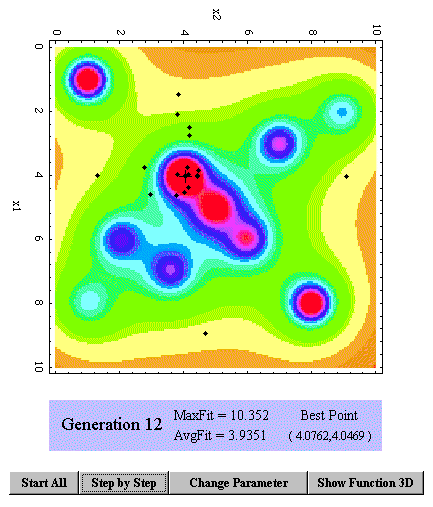
Fig. 8: Distribution of the individuals of population P(12)

The best search point of P(12) which is distinguished from the other ones by a little cross already represents a very accurate approximation of the global optimum point.

The animation example described above gives a detailed insight into the complex search process of Genetic Algorithms. It enables the user

to analyze the GA behaviour at extreme parameterizations (crossover rate=0, mutation rate=1, etc.);
to evaluate design alternatives of the genetic operators;
to adapt the GA optimally to specific optimization problems.

In order to make our animation environment available on the World Wide Web we have implemented it as a Java-applet. Fig. 5, 6, 7, and 8 give an impression of the graphical user interface of the first realization of the animation environment. At this very first stage of development only a Genetic Algorithm was implemented and just one goal function was available. This admittedly very simple applet however has been proven to be very intuitive, easy to handle, and a good entry for inexperienced users. For that reason we have decided to retain it in this publication, although there has been a much more sophisticated version realized meanwhile. The simple version of our animation environment is available as a Java-applet here or on the World Wide Web at: http://goethe.ira.uka.de/~syrjakow/viewapplet.html.

Beside a population-based Genetic Algorithm the extended version comprises an implementation of a point-to-point working Simulated Annealing algorithm. The object-oriented design of our animation environment incidentally makes it very easy to integrate further direct optimization algorithms. The graphical user interface was also modified and extended significantly. Here the most important new features are

a text area printing a detailed optimization trace during animation,
more possibilities to interactively control the animation,
an opportunity to visualize and compare optimization trajectories computed by different optimization algorithms.

The extended version of our animation environment is available as a Java-applet here or on the World Wide Web at: http://goethe.ira.uka.de/~syrjakow/viewenvapplet.html.

In our future work we intend to add further optimization algorithms (not only probabilistic ones but also deterministic Hill-Climbers) to our animation environment as well as to enlarge the set of goal functions. Beside that we want to equip the graphical user interface with more functionality. In this context a worthwhile feature would be a possibility for visualization of evolving convergence measures. Successor versions of our animation environment will be announced on the World Wide Web at: http://goethe.ira.uka.de/~syrjakow/animations.html.

CONCLUSIONS

In this paper the SW-architecture of an animation environment for probabilistic search algorithms was presented. The intended purposes of this environment are

to give deep an illustrative insights into the complex search processes of probabilistic optimization algorithms;
to support the research work on stochastic search techniques;
to help inexperienced users to understand how probabilistic optimization works.

To demonstrate its capabilities the animation environment was applied to visualize the evolving data structure of a Genetic Algorithm. Beyond GAs our animation approach can be easily applied to visualize other direct optimization methods. This and the fact that parameterizable implementations of probabilistic algorithms are considered for animation can be viewed as the special merits of our approach.

For the future we intend to add more functionality to the visualization component that should enable us to further increase our knowledge about stochastic search processes. Beyond that we plan to extend the animation environment with some more probabilistic search algorithms (Evolution Strategies, Monte-Carlo search) as well as with deterministic Hill-Climbing methods.

ACKNOWLEDGEMENTS

We want to thank Prof. D. Schmid for his encouragement and support of our work. We also thank our students, especially C. Bentz and B. Zimmermann for their engagement and contributions.

REFERENCES

Aarts, E.; and J. Korst. 1990. Simulated Annealing and Boltzmann Machines. Wiley.

Flanagan, D. 1996. Java in a Nutshell. A Nutshell Handbook. O'Reilly.

Goldberg, D.E. 1989. Genetic Algorithms in Search, Optimization and Machine Learning. Addison-Wesley.

Michalewicz, Z. 1992. Genetic Algorithms + Data Structures = Evolution Programs. Springer.

Schaffer, J.D.; R.A. Caruana; L.J. Eshelman; and R. Das. 1989. "A Study of Control Parameters Affecting Online Performance of Genetic Algorithms for Function Optimization." Proceedings of the third International Conference on Genetic Algorithms. June 4-7. George Mason University. pp. 51-60.

Schwefel, H.-P. 1981. Numerical Optimization of Computer Models. Wiley.

Shekel, J. 1971. "Test Functions for Multimodal Search Techniques." Fifth Annual Princeton Conference on Information Science and Systems.

Stasko, J.T.; J.B. Domingue; M.H. Brown; and B.A. Price (eds.). 1998. Software Visualization. The MIT Press.

Syrjakow, M.; and H. Szczerbicka. 1995. "Simulation and Optimization of Complex Technical Systems." Proceedings of the 1995 Summer Computer Simulation Conference SCSC'95. Ottawa. Ontario. Canada. July 24-26. pp. 86-95.

BIOGRAPHY

Helena Szczerbicka was born in Poland. She received the M.Sc. in applied Mathematics and the Ph.D. in Computer Science from the Technical University of Warsaw, Poland, in 1974 and 1982, respectively. In July 1985 she joined the Faculty of Computer Science at the University of Karlsruhe, West Germany. Since 1989 she has been with the Institute of Computer Design and Fault-Tolerance at this faculty as an Associate Professor. Since May 1994 she has been a professor in computer science at the University of Bremen, Germany. More information is available at http://www.informatik.uni-bremen.de/grp/ag-ram/helena.html.

Michael Syrjakow was born in 1964, in the Federal Republic of Germany. He received the Dipl.-Inform. degree from the University of Karlsruhe, Germany in 1991. Since then he has been with the professional group Performance Modelling at the Institute of Computer Design and Fault-Tolerance, University of Karlsruhe, Germany. In February 1997 he received the Ph.D. in Computer Science from the University of Karlsruhe, Germany. More details can be found at http://goethe.ira.uka.de/~syrjakow/.