REMO - REsearch Model Optimization Package

 

Michael Syrjakow
Institute for Computer Design and Fault
Tolerance (Prof. D. Schmid)
University of Karlsruhe, 76128 Karlsruhe,
P.O. Box 6980, Germany
E-mail: syrjakow@ira.uka.de
Helena Szczerbicka
Department of Computer Science
(Fb3 Informatik)
University of Bremen, 28334 Bremen,
P.O. Box 330440, Germany
E-mail: helena@informatik.uni-bremen.de
 

1 Introduction

The software tool REMO (REsearch Model Optimization Package) was primarily developed to automate the process of model optimization. It comprises a library of powerful direct optimization algorithms which are applicable to both parameter optimization of analytical and simulation models. Direct optimization means that only goal function values are required to guide the optimization process. Additional analytical information like gradients, etc. is not used. Beside the optimization algorithms REMO provides an interface to connect it with conventional modelling tools. Together with a modelling tool REMO enables the user

· to implement and to analyse the model which has to be optimized,

· to specify the optimization problem,

· to automatically perform the model optimization process.

 
Fig. 1: Architecture of REMO

 

2 Architecture

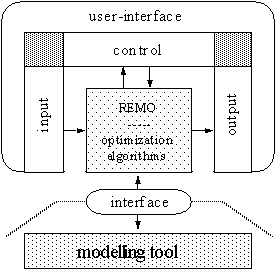
The architecture of the model optimization tool REMO is presented in Fig. 1. The basic components are:

1) a graphical user-interface, which is composed of an input-, control-, and output part,

2) a library of powerful direct optimization algorithms,

3) an interface for coupling REMO with a conventional modelling tool.

 REMO is currently running on SUN-SPARCstations 10 with Solaris 2.5. The realization of the graphical user-interface is based on the XView (X Window-System-based Visual/Integrated Environment for Workstations) - libraries.

 

3 Functionality

In the following the functionality of each component of REMO is explained in detail.

 

3.1 Graphical User-Interface

When working with REMO, the user has to handle a multitude of input parameters and to cope with a high quantity of output data, generated during the optimization process. In order to get a well structured user-interface, which is easy to survey, it was subdivided into an input-, control-, and output part.

 

Input Part

The input part enables the user to specify optimization experiments. Such a specification comprises the following aspects:

· specification of the optimization problem (goal function, search space, parameter constraints, etc.),

· choice of an appropriate optimization strategy,

· adjustment of the control parameters of the applied optimization method,

· choice of different possibilities for visualization of the optimization process (textual or graphical),

· specification of size and kind (screen and/or file) of the optimization output report which informs about the optimization effort, result, and trajectory.

 

 Control Part

The control part enables the user to interactively control the running optimization process. For that purpose possibilities

· to switch over to a step mode for better observation of the optimization process,

· to modify the step size of the step mode,

· to modify control parameters of the running optimization algorithm,

· to skip a phase of the optimization process to avoid inefficiencies,

· to force the output of provisional results,

· to stop the running optimization process prematurely

 are provided.

 

Output Part

The main tasks of the output part are

· visualization of the optimization process This feature enables the user, if necessary, to manipulate the optimization process interactively using the control part. At the moment, the user can choose between five different output report modes. Additionally, different file report modes allow to save generated optimization data onto file. · presentation of the optimization results After termination of an optimization run the optimization result (best found solution of the optimization problem) and the optimization effort (number of required goal functions evaluations) are displayed on screen and/or saved onto file. Optionally it is possible to display the optimization trajectory (all solutions generated during the optimization process).

 

 3.2 Library of direct optimization algorithms

REMO offers to the user an extensive library of direct optimization algorithms. Table 1 comprises the basic components of this library. Genetic Algorithms [2] and Simulated Annealing [1] represent powerful strategies for global optimization. The Pattern Search Algorithm of Hooke and Jeeves [3] is a very efficient local Hill-Climber. Outgoing from these basic components (so-called atomar strategies) the user can compose more sophisticated optimization methods (combined 2-phase optimization strategies or multiple-stage optimization strategies).

 

global
local
Genetic Algorithms
Simulated Annealing
Pattern Search Algorithm
of Hooke and Jeeves
Table 1: Atomar optimization strategies of REMO

 

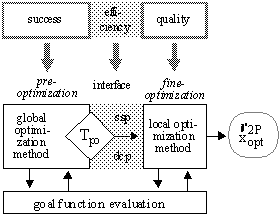
To be able to cope with the non-trivial task of model optimization we have developed a new class of direct optimization algorithms called combined 2-phase strategies. These strategies are based on the splitting of the optimization process into two phases: pre-optimization with a probabilistic global optimization method and fine-optimization performed by a deterministic local Hill-Climber. The task of pre-optimization is to explore the search space in order to find promising regions where global optimum points might be located. Outgoing from the results of pre-optimization the task of fine-optimization is to localize the optimum point in a promising region efficiently and exactly. Thus, pre-optimization is predominantly responsible for optimization success, whereas fine-optimization has to ensure optimization quality. Fig. 2 shows the basic structure of a combined 2-phase optimization strategy. The global optimization method is coupled with the local optimization method by means of an interface, comprising a method to derive control parameter values from optimization trajectories (dcp) as well as a method to select start points (ssp). After termination of pre-optimization by Tpo the task of dcp and ssp is to compute a favourable starting condition for fine-optimization.

 

Fig. 2: Basic structure of a combined 2-phase optimization strategy

 

Outgoing from the atomar global and local optimization methods presented in Table 1 there exist the following possibilities to realize a combined 2-phase strategy:

· Genetic Algorithm + Pattern Search,

· Simulated Annealing + Pattern Search.

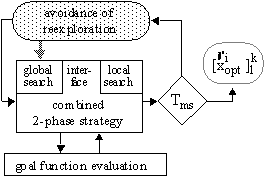
 More details about combined 2-phase strategies as well as optimization results are described in [4], [5] and [6].

All optimization methods presented so far can be used for single-stage optimization within a multiple-stage optimization method. Multiple-stage optimization means that a single-stage method is executed several times successively in order to generate a sequence of optimum points. To avoid that previously found optimum points are located again in subsequent optimization stages a method called avoidance of reexploration is applied. The basic structure of a multiple-stage optimization algorithm using a combined 2-phase strategy for single-stage optimization is shown in Fig. 3. A more detailed description of multiple-stage optimization can be found in [6].

 

Fig. 3: Basic structure of a multiple-stage optimization strategy

 

For special adaptation of the implemented optimization algorithms to intricate model optimization problems the software tool REMO offers supplementary methods for

· acceleration of the optimization process by goal function approximation,

· enhancement of the robustness against goal functions which are heavily distorted by stochastic inaccuracies.

 

 3.3 Interface to couple REMO with modelling tools

In order to automate the process of model optimization a coupling of optimization and model analysis has to be realized. Therefore a specific interface was developed, comprising a data and a synchronisation part [4]. Input parameters and goal function values are exchanged using the data part. Synchronisation signals which manage the alternated switching between optimization and model analysis are exchanged using the synchronisation part.

 

4 Conclusions

REMO (REsearch Model Optimization Package) represents a software tool for optimization of analytical and simulation models. For that purpose REMO comprises a library of powerful direct optimization algorithms. Basic components of this library are atomar strategies which can be put together to more sophisticated methods like combined-2-phase and multiple-stage optimization strategies.

Combined-2-phase strategies try to combine the advantages of global and local search, i.e.

· to achieve a high success rate (high probability of finding the global optimum),

· to generate optimization results which satisfy user-specified quality demands,

· to ensure high efficiency.

 The excellent heuristic properties of a combined 2-phase strategy can be viewed as the basic requirement for multiple-stage optimization. Here the most important goals are · to monotonously increase the optimization success with every optimization stage,

· to generate heterogeneous sequences of optimum points,

· to localize the most prominent optimum points in early optimization stages.

 Altogether, combined 2-phase and multiple-stage optimization can be viewed as a substantial improvement compared to existing direct optimization methods like Genetic Algorithms, Simulated Annealing, and Pattern Search. Encouraging results, obtained with our optimization methods can be found in [4], [5] and [6]. The results show that our approach is not only applicable to mathematical test problems but also qualified for parameter optimization of expensive to evaluate simulation-based goal functions.

 

References

[1] Aarts, Emile; Korst, Jan: Simulated Annealing and Boltzmann Machines; John Wiley & Sons, 1989.

[2] Goldberg, D.E.: Genetic Algorithms in Search, Optimization and Machine Learning; Addison-Wesley, 1989.

[3] Hooke, R.A.; Jeeves, T.A.: Direct Search Solution for Numerical and Statistical Problems; Journal ACM 8, pp. 212-221, 1961.

[4] Syrjakow, M.; Szczerbicka, H.: Optimization of Simulation Models with REMO; Proceedings of the European Simulation Multiconference ESM'94, Barcelona, Spain, June 1-3, 1994, pp. 274-281.

[5] Syrjakow, M.; Szczerbicka, H.: Simulation and Optimization of Complex Technical Systems; Proceedings of the 1995 Summer Computer Simulation Conference SCSC'95, Ottawa, Ontario, Canada, July 24-26, 1995, pp. 86-95.

[6] Syrjakow, M.; Szczerbicka, H.: Combination of Direct Global and Local Optimization Methods; Proceedings of the International Conference on Evolutionary Computing ICEC' 95, Perth, Western Australia, November 29 - December 1, 1995.
 
 

Back to the Homepage